4. N-tuple Analysis using RhoTuple¶
4.1 Effective Analysis with ROOT TTrees¶
After we spent a lot of time about how to write out ROOT TTrees rather then storing histograms, I’d like to point out why all this.
User analyses very often store histograms as a result of the analysis macro code. While this can be a good idea in case one finalizes the analysis and applies nice formatting to the plots, it has quite some disadvantages in the course of the analysis. These are, that you
can’t change to finer binning (to detect small scale features)
can’t change the region of interest
can’t check impact of related cuts
can’t study correlations between observables
can’t study additional variables not put to histograms.
In order to overcome all these limitations above, the solution is to store a ROOT TTree instead, or at least in addition. A TTree basically is a large table, where each event or reconstructed candidate represents one line in the table. Once you have it generated, you can work interactively with it to get familiar with the data. For a comprehensive documentation please visit https://root.cern.ch/root/htmldoc/guides/users-guide/Trees.html.
The most powerful methode of this object is TTree::Draw. It generates auto-range histograms in 1D, 2D and even 3D
on the fly, allows to study apply selection cuts, correlate variables and has many visualization features. The following
list shows just very few examples:
root[0] ntp->Draw("var1") // distribution of var1 (auto-range)
root[1] ntp->Draw("var1:var2") // correlation of var1 and var2
root[2] ntp->Draw("var1","var2<1") // draw under condition var2<1
root[3] ntp->Draw("var1>>h(20,2,5)") // draw to histo with 20 bins, range [2..5]
root[4] ntp->Draw("sqrt(var1+var2^2)") // compute formula for each entry
root[5] ntp->Draw("var1:var2","","col") // color map instead scatter plot
root[6] ntp->Draw("var1","","",100) // first 100 entries only
4.2 Using RhoTuple¶
In addition to store the analysis results in histograms, I’m personally much in favour of working with N-Tuples instead (or at least in addition). This allows you continue and refine your analysis interactively in CINT and gives you a ‘feeling’ for the data very quickly.
In Rho there is a quite handy class called RhoTuple (http://panda-wiki.gsi.de/cgi-bin/view/Computing/PandaRootAnalysisJuly13) to simplify the cumbersome dealing with trees and ntuples in ROOT by creating branches and setting branch addresses. After creating an object with
RhoTuple *ntp = new RhoTuple("ntp","J/psi analysis");
there are only two relevant methods which you need to know:
ntp->Column("name", var, defaultval);
This either fills the branch "name" with value var or creates and fills it, if is not yet
existing. Because of this autmatism, there is no need to think and prepare beforehand what quantities
you might want to store, as you need to do if handling the TTree yourself.
The default value defaultval is written to the branch if you don’t fill explicitly the branch for
some events. Here you should make sure that all branches you want to use have been created from the
beginning, otherwise you might have an inconsistent ntuple, since for some events not all branches
are available.
Just filling the branch with a certain value does not already finally store it. It’s basically just setting the variable assigned to the corresponding branch address handled by RhoTuple internally. In order to store all existing branches, i.e. fill the TTree with current values, you need to call the second relevant method
ntp->DumpData();
This really writes numbers to the tree.
The following code snippet demonstrates the usage for our example analysis. Let’s say, we want to store information about our J/psi in order to optimize the selection. This could look like:
RhoTuple *ntp = new RhoTuple("ntp","J/psi analysis");
...
// ... in event loop ...
for (j=0; j<jpsi.GetLength(); ++j)
{
// *** store event number and candidate number in current event
ntp->Column("ev", (Float_t) evnumber, -999.0f);
ntp->Column("cand", (Float_t) j, -999.0f);
// *** basic information about J/psi
ntp->Column("jpsim", (Float_t) jpsi[j]->M(), -999.0f);
ntp->Column("jpsip", (Float_t) jpsi[j]->P(), -999.0f);
ntp->Column("jpsipt",(Float_t) jpsi[j]->P4().Pt(), -999.0f);
ntp->Column("jpsiE", (Float_t) jpsi[j]->E(), -999.0f);
// *** prepare pointers to daughters and their reco candidates
RhoCandidate *mup = jpsi[j]->Daughter(0);
PndPidCandidate *mupr = (PndPidCandidate*)mup->GetRecoCandidate();
// *** info from daughters
ntp->Column("mupp", (Float_t) mup->P(), -999.0f);
ntp->Column("mupiron", (Float_t) mupr->GetMuoIron(), -999.0f);
// *** finally fill ntuple
ntp->DumpData();
}
...
// ... end of macro ...
TFile *f=new TFile("ntp.root","RECREATE");
ntp->GetInternalTree()->Write();
f->Close();
Note that the variables have to be casted properly, since the method =Column= has many overloaded ones for the different data types like bool, int, etc.
After running your analysis macro or task and storing the ntuple in the output file, you can work with it in CINT. The example macro tut_ana_ntp.C shows some more ideas how to store which kind of information for further n-tuple analysis.
4.3 The QA-Tools¶
Since in physics analysis people want to store always the same kind of variables like invariant masses,4-vector components, PID information, fitter results, MC truth info, or even full decay tree information of complex composite candidates and event shape variables, it pretty obvious to simplify the storage of these kind of information. Therefore a handy tool is provided, which allows to compactly dump out all these kind of data, called PndRhoTupleQA.
This class provides a large number of methods to store multiple quantities at once. The most commnon ones probably are (for a complete documnetation take a look at https://panda-wiki.gsi.de/foswiki/bin/view/Computing/PandaRootAnalysisJuly13#PndRhoTupleQA):
// 4-vector, position, charged, pdg-code
void qaCand(TString pre, RhoCandidate *c, RhoTuple *n);
// recursive decay tree data
void qaComp(TString pre, RhoCandidate *c, RhoTuple *n);
// store 4-vector and position information
void qaP4(TString pre, TLorentzVector c, RhoTuple *n);
void qaP4Cms(TString pre, TLorentzVector c, RhoTuple *n);
void qaPos(TString pre, TVector3 p, RhoTuple *n);
// pid, vertex, decay
void qaPid(TString pre, RhoCandidate *c, RhoTuple *n);
void qaVtx(TString pre, RhoCandidate *c, RhoTuple *n);
void qa2Body(TString pre, RhoCandidate *c, RhoTuple *n);
void qaDalitz(TString pre, RhoCandidate *c, RhoTuple *n);
// fitter information
void qaFitter(TString pre, RhoFitterBase *fitter, RhoTuple *n);
// raw detector values
void qaRecoShort(TString pre, RhoCandidate *c, RhoTuple *n);
// MC information
void qaMcList(RhoTuple *n, int max = 10000);
void qaMc(TString pre, RhoCandidate *c, RhoTuple *n);
The usual parameters are a name prefix "pre", that is prepended to all quantities, the source
object (here c, p or fitter), and the RhoTuple n. For example, with prefix
"ppb_", the invariant mass is store as "ppb_m", the momentum as "ppb_p".
The most powerful methode is given by qaComp, which dumps rather complete information of a
reconstructed decay of a composite. In this example this single call generates 180 branches with all
kind of information. The strategy is to loop through the reconstructed decay tree
and call qaCand, qaP4Cms and qaPid for each final state, and qa2Body and qaDalitz
for all two- and three-body decays, respectively. In addition, it stores the MC-truth-match
information. For the i-th daughter, the method qaComp is called recursively, where di is
appended to the prefix.
In our example ppbar -> J/psi pi+ pi- -> mu+ mu- pi+ pi-, the mass of the
J/psi would be named "ppb_d0m", the pion PID of the pi+ "ppb_d1pidpi", the x-component of
the momentum of the mu- "ppb_d0d1px", and so on.
So if you don’t know what infos to store, just use the method qaComp on intermediate or final
composites. The macro tut_ana_compact.C would represent the full featured analyse for our example channel using
the QA-tool.
A typical use case and minimum example for an analysis could look like this (compare to macro tut_ana_mini.C):
RhoCandList muplus, muminus, piplus, piminus, jpsi, psi2s, all, neut;
RhoTuple *npsi2s = new RhoTuple("npsi2s", "psi(2S) Analysis");
PndRhoTupleQA qa(theAnalysis, 6.231552);
int i=0, j=0;
while (theAnalysis->GetEvent() && i++ < nevts) {
// *** fill lists for combinatoric
theAnalysis->FillList(muplus, "MuonAllPlus", pidSelection);
theAnalysis->FillList(muminus, "MuonAllMinus", pidSelection);
theAnalysis->FillList(piplus, "PionAllPlus", pidSelection);
theAnalysis->FillList(piminus, "PionAllMinus", pidSelection);
// *** perform combinatorics
jpsi.Combine(muplus, muminus, DB_jpsi); // J/psi -> mu+ mu-
theAnalysis->McTruthMatch(jpsi); // truth match of whole list
psi2s.Combine(jpsi, piplus, piminus, DB_pbps); // pbarp -> J/psi pi+ pi-
theAnalysis->McTruthMatch(psi2s); // truth match of whole list
for (j = 0; j < psi2s.GetLength(); ++j) {
// *** common event info
npsi2s->Column("ev", i); // event number
npsi2s->Column("cand", j); // candidate number
qa.qaP4("beam", ini, npsi2s); // beam 4-vector
// *** candidate specific info
qa.qaComp("pp", psi2s[j], npsi2s); // composite info
qa.qaMc("pp", psi2s[j], npsi2s); // 4-vector of truth match
// *** decay tree fitter
RhoDecayTreeFitter fittree(psi2s[j], ini); // setup fitter
fittree.Fit(); // perform fit
qa.qaFitter("fdc_", &fittree, npsi2s); // chi2 / prob
qa.qaCand("fpp", psi2s[j]->GetFit(), npsi2s); // fitted psi(2S)
qa.qaCand("fj", psi2s[j]->Daughter(0)->GetFit(), npsi2s); // fitted J/psi
// *** and finally FILL Ntuple
npsi2s->DumpData();
}
}
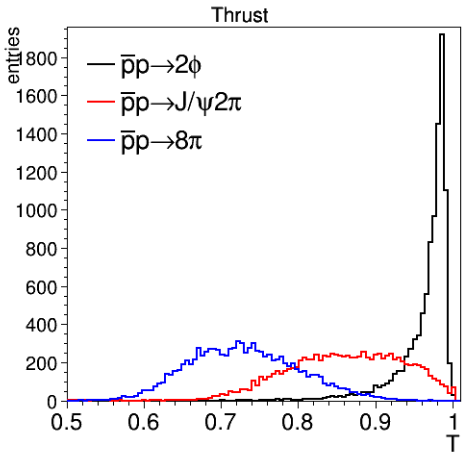
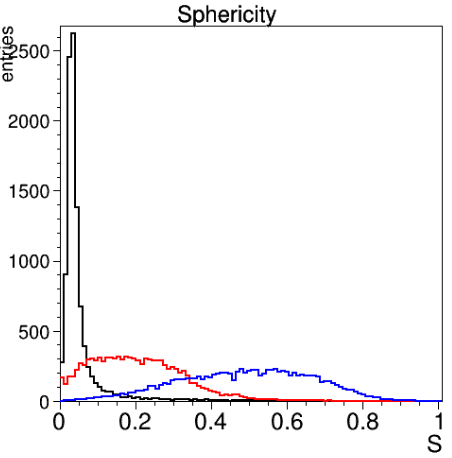
In combination with the PndEventShape object, which provides the functionallity to calculate many different event based quantities like e.g. thrust, sphericity, Fox-Wolfram-moments, multiplicities and many more
// create a list with all charged and neutral candidates
theAnalysis->FillList(all, "Charged");
theAnalysis->FillList(neut, "Neutral");
all.Append(neut);
// event shape calculator with threshold for: E(gamma) / p(tracks)
// v v
PndEventShape *evsh = new PndEventShape(all, ini, 0.03, 0.1);
the following QA-routines are also quite handy:
// event shape
void qaEventShape(TString pre, PndEventShape *evsh, RhoTuple *n); // all event variables
void qaEventShapeShort(TString pre, PndEventShape *evsh, RhoTuple *n); // reduced set of vars
The pictures below show two examples for event shape variables, thrust and sphericity. Obviously the more jet like events of pbar p -> phi phi show larger thrust and smaller spherictiy than the rather isotropic pbar p -> 8 pi+- events.